「2011 年 3 月 11 日，日本東北外海發生規模 9.0 的大地震，日本群島幾乎所有地區都觀測到了強度1級到6級弱的地震。宮城縣栗原市紀錄了最大強度7級(圖一)。」類似這種地震通報表示方式相信大家都不陌生，然而如果翻開各國地震中心的速報，會發現同一場地震另有 M_w9.1、M_s8.4、M_JMA 9.0各種不同的數值出現，還有強度(Intensity)7級的敘述，為何有這些不同？「規模」這個看似簡單的指標，背後藏著迥異的計算公式：有的方法取最大振幅，有的會根據物理特性，也有依本土經驗修正產生。於是，一場地震瞬間冒出多套數字，令人霧裡看花。

本期電子報將拆解芮氏、地震矩、表面波、體波等主流規模，說明不同地震規模指標所使用的計算方法，又該如何在媒體標題與官方報告間快速判讀真正的「能量大小」。了解世界各國最常用、也最容易被混淆的地震規模系統。

在 1935 年 Charles F. Richter 提出「芮氏規模(magnitude)」以前，地震大小的判斷全靠宏觀來判定，也就是觀察房屋破壞與人體感受的主觀描述。19 世紀之前，各地雖嘗試將這些描述加以分類，卻缺乏統一標準。到了 19 世紀末，義大利的 De Rossi 與瑞士的 Forel 首度建構出十級制的 Rossi–Forel 震度表，為地震搖晃分級帶來較完整的架構，但當時的地震儀僅能協助確認最低一級，整體仍偏重文字敘述(圖二)。

20 世紀初，義大利火山學家 Giuseppe Mercalli 受此啟發，於 1902 年提出十二級制的 Mercalli 震度表，從「無感」至「全毀」細分 I–XII 級，並在隨後多次修訂成為今日沿用的「修訂麥卡利震度分級(圖三)」。雖然有這些分級方法可以讓人們得知主觀地震大小，但缺乏一套統一的「能量」以及客觀的測量地震大小的方法，所以1935年芮氏規模的出現，把「地震大小」從主觀破壞描述，正式推進到可比較、可換算能量的定量時代。

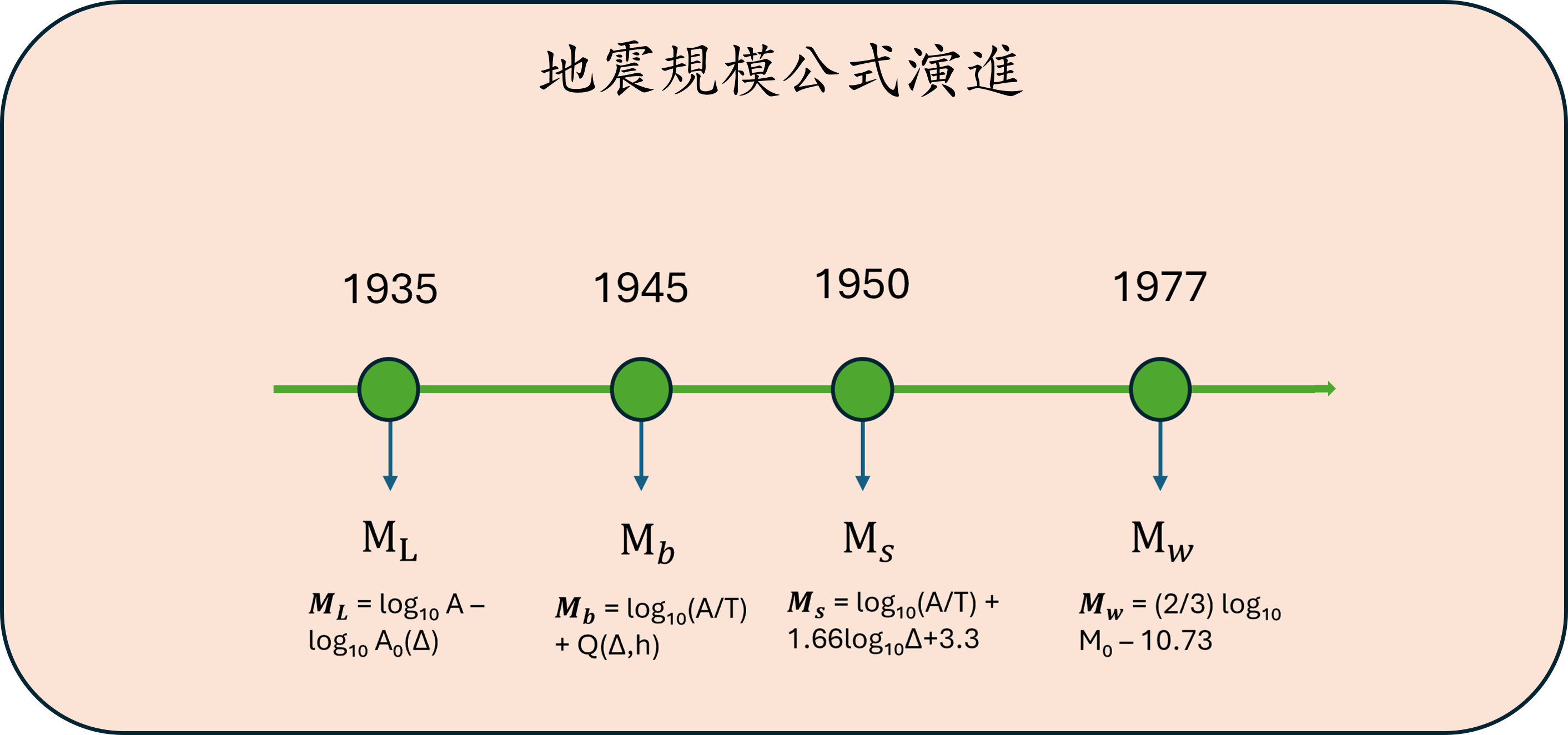
如圖四所示，1935年出現關於地震規模的定義以及計算方法，此方法為芮氏規模，亦稱近震規模(local magnitude，M_L)，由Charles F. Richter 在美國加州短週期地震儀推導：M_L = log₁₀ A – log₁₀ A₀(Δ)。其中A =在某觀測站所記錄之最大振幅(以μm為單位，1μm= 10-6 m)、A₀(Δ)=距離修正量；當地震儀於距離震央100公里處紀錄標準地震之最大振幅。

一開始只適合在美國加州使用，後續經過各國修正「利用地震觀測網內各地地震站儀器收錄到同一地震之紀錄，分別修正距離、計算規模後，再進行數值平均來演算出該次地震之規模」，適用於世界各國。但由於當初設計芮氏地震規模時所使用地震儀的限制，當芮氏地震規模大於7.5時會有「飽和」現象，也就是計算出來的所有地震規模值都趨近相同，另外當距離震央超過600公里，超出後的衰減誤差會有放大效應，所以在地震規模不大(不超過7.5)的情況下，因其計算速度快，時至今日仍是我國氣象署速報所使用的規模計算方式。

1945年出現了體波規模(body wave magnitude，M_b)的計算方式，此方法是使用P波的振幅來計算地震的規模(Measuring the Size of an Earthquake)。P波是一種以5到8 km/s在整個地球中傳遞並且通常是最早到達地震儀的地震波。因此，計算體波的強度是確定遠距離地震規模最快的方式。公式為M_b = log₁₀(A/T) + Q(Δ,h)，在這裡A是地表運動的幅度（單位微米），T是體波週期（單位秒），Q(Δ,h)是距離函數的修正係數，Δ是震央和地震測站夾角（單位角度），h是震源深度（單位公里）。但當M_b大於6.5即會發生飽和，因此比芮氏規模更加不適合使用於大型地震的規模測量，適用於較小型的地震事件。

1950年代出現以表面波來計算規模的方法，稱為表面波規模(Surface wave magnitude，M_s)，公式為M_s = log₁₀(A/T) + 1.66log₁₀Δ+3.3，其中A和T分別是體波的波幅和週期，透過量度地震波波形可得。而Δ是測站離震央距離。此方法專為遠震設計(220km < Δ < 17,800km)，當距離小於220km反而無法使用，此方法可以測得的M_s上限可以到達8.5，目前在歐洲以及南美較為常見使用。

再來是目前全世界最為通用的規模計算方法，此方法在1977年提出---地震矩規模(moment magnitude scale，M_w)，公式為M_w = (2/3) log₁₀ M₀ – 10.7，M₀代表地震矩，是地震學家用來表示地震所釋放出之能量的數量，定義為：M₀=μＤＳ，μ為斷層物質之剛性係數(rigidity或shear modulus)、Ｄ為斷層之平均滑動量 (位移)、Ｓ為斷層面積。可以明顯看出與前面三個有非常大的不同，是與震源相關的物理特性有著直接關係，並且此方法沒有規模上限的存在，但通常M_w不太可能出現10以上的數字，因為斷層長度會高達上萬公里，相當於地球1/4的周長，在USGS(美國地質調查局)、GFZ(德國地理研究中心)、EMSC(歐洲與地中海地震中心) 等全球報告皆以 M_w 為主。

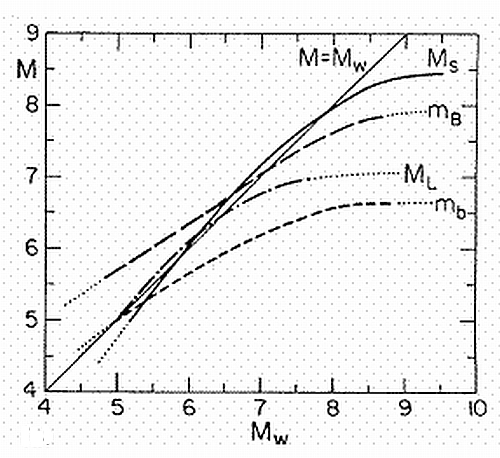
常見錯誤迷思是直接將兩個不同方法計算出來的規模進行比較，舉一個例子：M_w 7.1是否等於M_L 7.1，答案是否定的，因為兩者的計算方法有著極大差異，即使是同樣的數字也代表著不同的能量大小，這裡可以透過圖五來進行不同規模之間的數值轉換。圖六為臺灣近年發生較大規模地震，以**地震矩規模(moment magnitude scale，M_w )及芮氏規模(local magnitude，M_L)**呈現的對照情形。

額外補充一個日本目前所使用的規模計算方式，此方法為M_JMA，有分為兩個版本，一個是主要針對震央距 ≤ 600 km 的「地方地震」，M_JMA = log₁₀(A_D) + β_D(Δ,H)+ C_D，其中A_D：加速度記錄積分所得的最大位移振幅（10^-6m），β_D：隨距離與深度遞減的修正項，C_D：常數；另一個是針對速報版本，滿足「M_w > 6.5、深度 ≤ 100 km、靠近海岸」等條件的地震，氣象廳為加速發布所使用的公式M_JMA=log₁₀(A_D)+log₁₀Δ+a₁Δ+a₂，a₁、a₂皆為常數，公式僅需少量 P 波資料即可估算，約 10 秒內即能在國內外海嘯警報中看到，與震度分級（0–7 級）換算最為便利，因此日本國內日常仍優先使用。

我國在2010年以前使用地震震度分為 8 級，其中在 5 級（強震）及 6 級（烈震）級距區間較寬，不利區分災情差別。隨著新建置之地震儀在量測的時間解析度增加，加上布建之地震站愈來愈密集，為強化地震震度在地震救災與應變作業上的實用性，氣象署研訂新制地震震度分級，將震度 5 級、6 級分別細分為 5弱、5強、6弱與6強，並修改5級以上地震震度分級之演算程序(由PGA加速度判定轉變為PGV速度判定)，使地震震度與災害發生有更高之關聯性，新制地震震度分級已於 2010 年 1 月 1 日起實施(圖七)。

地震規模每增1級，釋放能量通常相差32倍、地表波振幅則約增加10倍，但實際上地表破壞程度仍受震源深度、距離、地質、建築結構與品質等影響。在第114期電子報有提到，若地震預估規模到達5.0以上且震度有4級以上，會向民眾發布國家級警報。若地震規模到達7以上，在陸地震度6弱級以上的地區預計會有很大的災情產生，內政部即刻成立地震中央災害應變中心一級開設，接著利用第109期電子報所提到的應變管理資訊系統(EMIC)，有效且即時的掌握災情訊息及處理狀況，並且持續追蹤災區更新資訊，協助民眾進行疏散撤離與避難。

回到一開始的疑問：同一次日本2011年東北大地震為何同時出現 M_w 9.1、M_s 8.4、M_JMA 9.0，而 M_L 不見蹤影？關鍵在於計算方法不同。M_w以地震矩計算斷層面積 × 滑移量，是把整條斷層的能量計算；M_s、M_b、M_L 則分別用振幅做公式計算，當事件規模超過一定規模就會「飽和」，數字自然偏低。M_JMA在 M_L 基礎上加入日本本土速度構造與距離衰減修正，方便快速發布海嘯與震度資訊。另外因為各種規模就使用不同公式，各有適用場景，不能直接進行數字對比，想要了解整體地震能量，看 M_w 最能還原全貌。

1.「震」的搞錯了，並沒有「芮氏規模9.0」的地震！
2. 地震百問 27. 各種地震規模的計算值都是一樣的嗎?
3. 地震百問 26. 如何計算規模?
4. 日本氣象廳
5. USGS M 9.1 - 2011 Great Tohoku Earthquake, Japan
6. 當人類終於知道為什麼會地震：地震規模和震度的由來
7. 震度與地震大小無關？怎麼讓「震 知道了」？那些關於震度的二三事
8. Rossi-Forel scale of earthquake intensities
9. Modified Mercalli Intensity Scale