電子報
受限於設置條件及維運成本,集水區雨量站及流量站設置數量有限,以致難以精確觀測區內逕流量,常需透過經驗公式/數值模式進行估算。然而在缺乏實測值驗證下,如何快速評估所採用之模式工具的適用及準確性,將是一大挑戰。本期電子報將介紹美國環保署(US EPA)所彙整常見的降雨-逕流估算方法,探討如何在集水區中選擇一個適合的降雨-逕流模式。
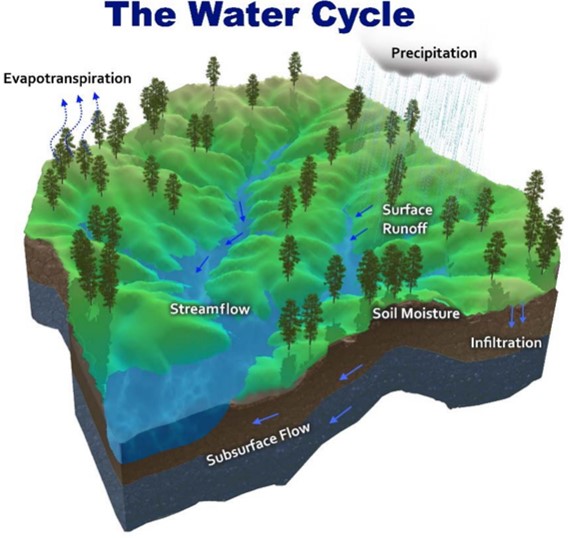
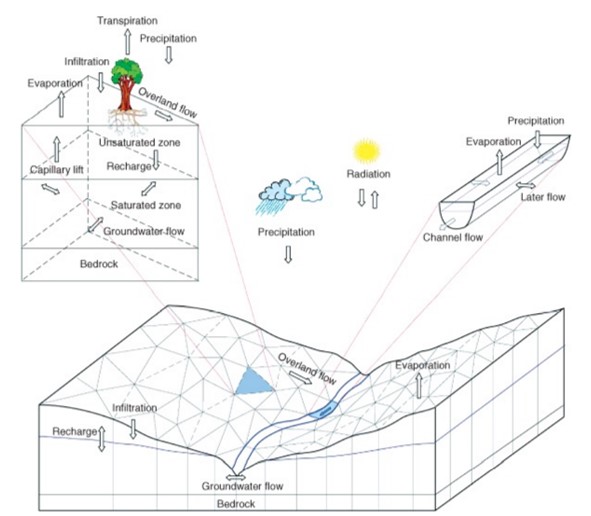
集水區中所謂的「逕流」,指的是降雨後未入滲到土壤,直接在地表流動的水,常見如野溪、河川、湖泊、水庫等(Perlman, 2016),逕流的產生是由於土壤過飽和及土壤超滲兩原因所致(Yang et al., 2015)。而從降雨變逕流過程僅是水循環中的一個部份,常以水平衡方程式表示如下:
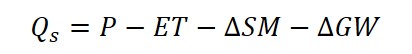
在水資源監測上,估算逕流量是一項重要的工作,如洪水預報評估洪水對下游保全對象的危害度。此外,集水區所產生之逕流亦將伴隨泥砂及污染物傳輸,進而影響下游環境,因此合理的估算逕流量對集水區管理而言將是一重要課題。
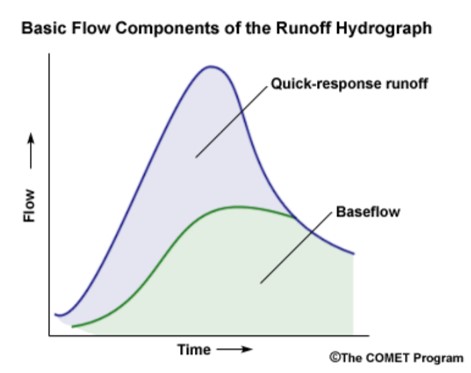
早在西元1851年,電腦數值模式還未發展成熟前,Thomas Mulvaney就以概念化模型-「合理化公式」(Rational Method)估算逕流量,藉由降雨強度、集流面積、逕流係數決定集水區的尖峰流量(Beven, 2012; Xu, 2002)。之後,「單位歷線」(Unit Hydrograph)法採疊加原理估算暴雨事件的逕流量,可分離河川中因暴雨所形成之逕流及基流量(Base Flow),如圖2.。隨著對水文過程的深入理解,逕流模式的開發也越來越精細。然而,因應不同事件,模式開發的目的性也不同,因此各模式各有其優勢與適用時機,一般在模式選定上,可依使用目的、資料取得難易度、計算時間成本、模式開發預算等來初步評估模式合宜性。
逕流量的計算將由模式開發架構所決定,依建構複雜度可區分為經驗公式(Empirical Model)、概念模式(Conceptual Model)、物理模型(Physical Model)等,各模式架構比較如表1.所示。
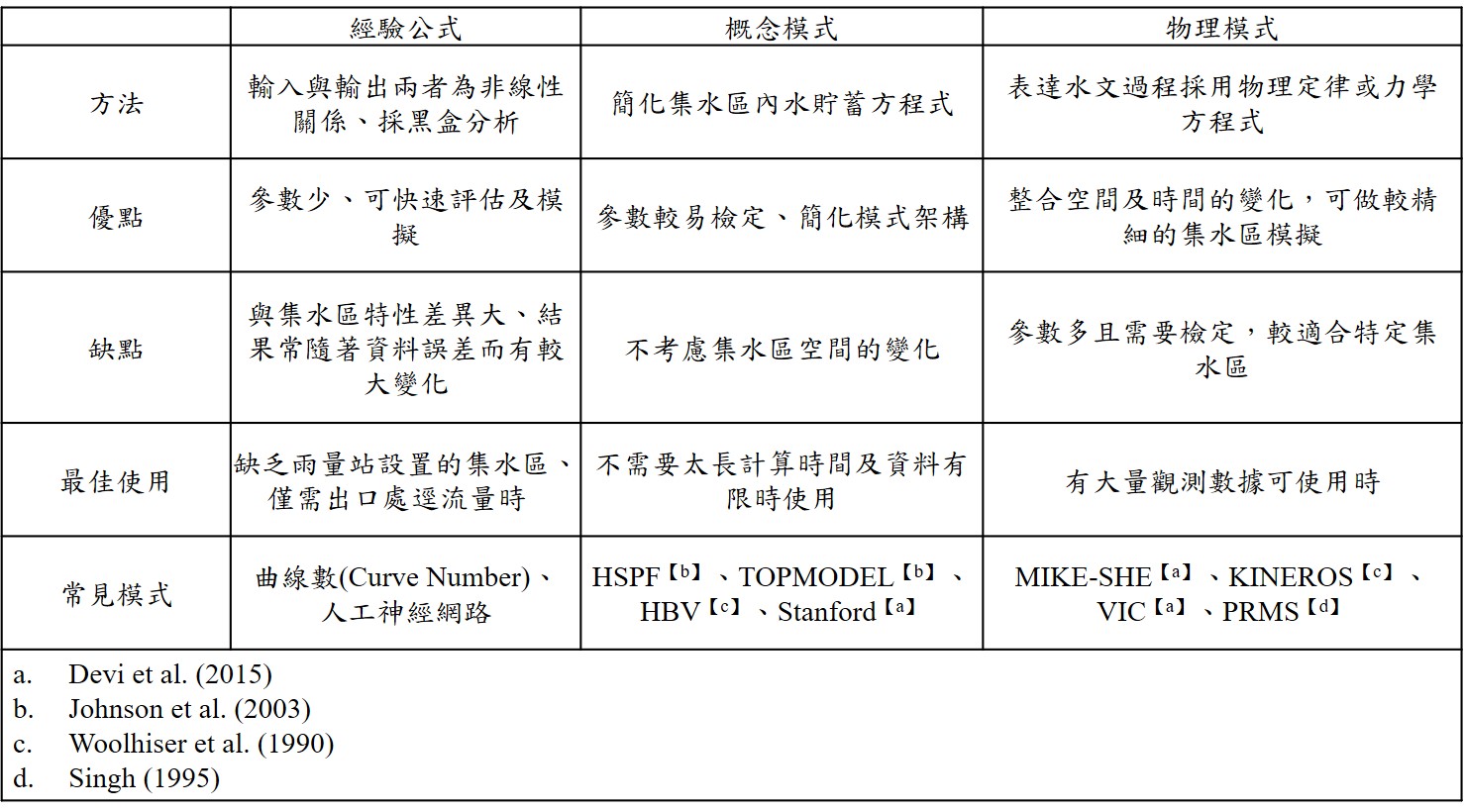
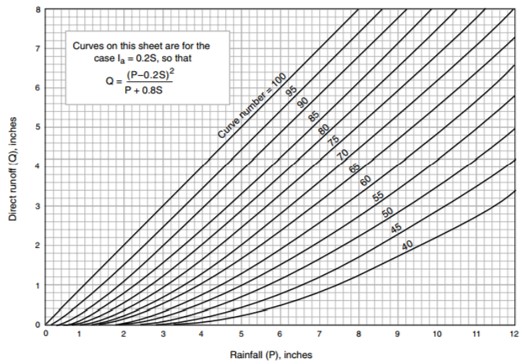
當缺乏雨量站及集水區資訊時,可採用經驗公式(Pechlivanidis et al., 2011),其所需參數較少,具有簡化、快速計算、花費少的優點,但其採用黑盒分析,亦即內部運算過程無法得知。經驗公式又稱為資料驅動(Data-driven)模式,亦即資料本身的正確性相當重要,錯誤的資料往往會導致結果有很大的偏估。常見以非線性統計方法來表示輸入(Input)與輸出(Output)兩者之間的關係,如圖3.所示降雨與逕流量的關係。
概念模式將水文循環過程簡化,也因諸多簡化程序,集水區在空間的變異性並不在模式考量中,另外,其控制方程式較缺乏物理意義,通常適用在較不需細部掌握集水區特性時。模式以降雨-逕流、蒸發散、地下水流動等彼此轉換關係來表示水平衡方程式,其控制方程式係將地表水及水庫儲蓄量變化代入水平衡方程式中,如下所示:
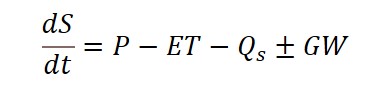
物理模型主要是依據水文循環的物理特性進行模式開發,控制方程式係依據水平衡方程式(Water Balance Equation)、質量、能量及動量守恆(Conservation of mass, energy, and momentum)、運動波(Kinematics)、聖維南(St. Venant)、波西尼斯克(Boussinesq’s)、達西(Darcy’s)以及理查德(Richard’s)方程式所得。例如將聖維南方程式的半離散形式整合於水文模擬系統中。
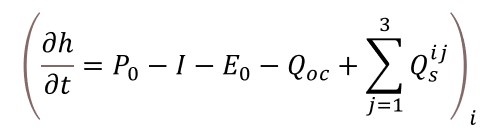
物理模型能模擬集水區在空間以及時間的變化,亦可模擬地下水流動、集水區內的泥砂、營養源、化學物質間的傳輸行為。模式經參數檢定後,模擬結果能有效反應出集水區特性,如圖4.所示。
逕流模式依空間結構變異程度如圖5.所示,可分成整合型(Lumped)、半分佈式(Semi-distributed)、分佈式(Fully distributed)模型。其中整合型模式不考慮集水區在空間上的變異性;半分佈式模式則能反應出集水區在某些空間的變異性;分佈式模式以網格點模擬集水區在空間的變異性,三者比較如表2.。
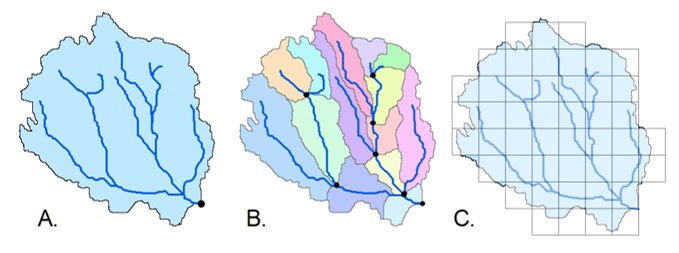
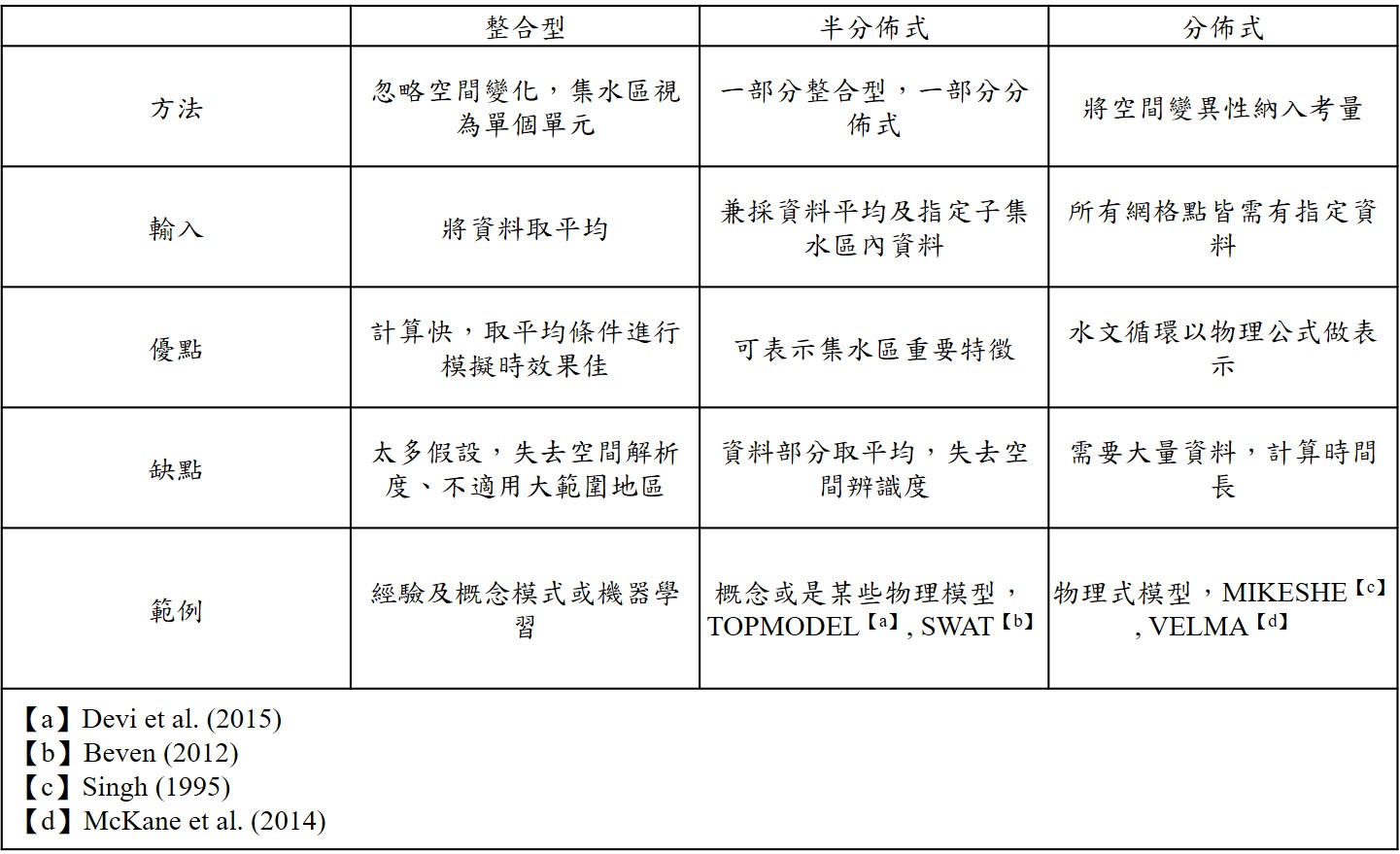
將所有集水區視為單一均質集水單元,集水區的空間變異性不納入考量,所有資料及變數均以單一平均值做代表,適合估算全流域單一出口處的逕流量。常見「經驗公式」及「概念模式」以整合模型來模擬水文於空間上的變化。
兼具整合型及分布式模型的特色。將集水區分成更小的集水區分別做計算,各子集水區擁有特定參數群,但其參數視為均一值,例如,各子集水區可以依照坡度、土壤組成、植生覆蓋不同特性來組成單一水文單元(Hydraulic Response Unit, HRU)。比起分佈式模式,使用半分佈式的優點是計算時間快,可用較少的資料及參數,缺點則是當使用網格點降雨資料,需取平均作使用,導致降雨在空間變異性無法被納入考量。常見「概念化模式」及「物理模式」採用半分佈式運行。
將空間的不同特性(異質性)納入考量,參數較多而複雜,其將集水區資訊透過網格點來進行計算,通常需要大量資料,如數值地形高程、土地使用圖層、網格點降雨量、土壤特性、集水區範圍及邊界條件等,其演算成果與真實情況最接近。分佈式模型的缺點就是每個格點上皆須有數據,如網格點欠缺數值,則須以外插(Extrapolation)來給定,分佈式模型受限於空間網格的解析度,運算時間可從幾分鐘到數個小時之久。
1. 降雨-逕流模式皆是簡化水文循環的過程來開發,模式大多需要參數檢定且存在著不確定性,加上集水區逕流量隨時間及空間改變,要準確估算集水區降雨-逕流量是不切實際的。舉例來說,隨著集水區內的植生覆蓋狀況、土壤含水量多寡、氣象條件及地表面條件狀況不同,逕流量也會有很大的變異。
2. 藉由降雨-逕流模式所得模擬成果,可掌握集水區逕流量因開發及環境變動時所帶來的變化。
3. 降雨-逕流模式可從開發複雜度及空間結構來區分,模式建置依控制方程式的複雜程度可分成經驗公式、概念模式、物理模型;依集水區空間結構建置時,可分成將流域視為單一單元的整合型模式、將流域劃分成子集水區來模擬的半分佈式模式及全流域以網格點做計算的分佈式模式。
4. 選定模式時,應考量計畫目的性、資料取得難易度、研究區域大小、需要輸出的變數及對結果的期望等來綜合做評估,例如集水區有高入滲率特性時,表示漫地流所產生之流量相對小,如選擇僅能計算漫地流而忽略地下水流動的模式時,則不適當(Knapp, 1991)。資料的精密度亦是模式選擇重點,當集水區缺乏精細資料,或者全域調查花費過於昂貴,則應以簡化模式為宜(Rinsema, 2014)。
- Beven, K. J. (2012). Rainfall-Runoff Modelling: The Primer (2nd ed.): Wiley-Blackwell.
2. Brewster, R. (2017). Paint.net 4.0.17(Version 4.0.17). Retrieved from https://www.getpaint.net/
3. Devi, G. K., Ganasri, B. P., & Dwarajish, G. S. (2015). A Review on Hydrological Models. Aquatic Procedia, 4, 1001-10017.
4. ESRI. (2015). ArcGIS Release 10.3.1 CA: Environmental Systems Research Institute.
5. Johnson, M. S., Coon, W. F., Mehta, V. K., Steenhuis, T. S., Brooks, E. S., & Boll, J. (2003). Application of two hydrologic models with different runoff mechanisms to a hillslope dominated watershed in the northeastern US: a comparison of HSPF and SMR. Journal of Hydrology, 284(1-4), 57-76.
6. Knapp, V., Durgunoglu, A., Ortel,T. . (1991). A Review of Rainfall-Runoff Modeling for Stormwater Management. U.S. Geologic Survey, Illinois District.
7. McKane, R., Brookes, A., Djang, K., Stieglitz, M., Abdelnour, A., Pan, F.,…Phillips, D. (2014). VELMA Version 2.0 User Manual and Technical Documentation Corvallis, Oregon
8. Pechlivanidis, I. G., Jackson, B. M., Mcintyre, N. R., & Wheater, H. S. (2011). Catchment Scale Hydrological Modelling: A Review of Model Types, Calibration Approaches and Uncertainty Analysis Methods in the Context of Recent Developments in Technology and Applications. Global NEST Journal, 13(3), 193-214.
9. Perlman, H. (2016, December 15). The Water Cycle- USGS Water Science School.
10. Qu, Y. (2004). An Integrated Hydrologic Model for Multi-Process Simulation using –discrete Finite Volume Approach. (Doctor of Philosophy), Pennsylvania State University.
11. Rinsema, J. G. (2014). Comparison of rainfall runoff models for the Florentine Catchment. University of Tasmania.
12. Singh, V. P. (1995). Computer Models of Watershed Hydrology Highlands Ranch, CO: Water Resources Publications.
13. UCAR. (2010). Runoff Modeling Concepts. Runoff Processes.
14. USDA. (1986). Urban Hydrology for Small Watersheds TR-55. Natural Resources Conservation Service.
15. Woolhiser, D. A., Smith, R. E., & Goodrich, D. C. (1990). KINEROS, A kinematic Runoff and Erosion Model: Documentation and User Manual. Agricultural Research Service.
16. Xu, C. Y. (2002). Hydrologic Models(Vol. 2). Sweden: Uppsala University Department of Earth Sciences Hydrology.
17. Yang, W.-Y., Li, D., Sun, T., & Ni, G.-H.(2015). Saturation-excess and infiltration-excess runoff on green roofs. Ecological Engineering, 74, 32-336.





